概述

这是一种神奇的算法——
首先解释一下KMP算法是干什么的。
你有两个长度不同字符串S、T，它们的长度分别为len1/len2，你要判断T是否为S的子串（即S中是否包含T）。
以人类的思维是是这样进行判断的：一位一位比较。然而这样速度太慢了，因为在最坏的情况下你最多可能需要比较进行(len1-len2) * len2次比较。
那你有没有思考，为什么会很慢呢?是因为在此过程中，你做了很多重复的工作，而KMP算法就是用来尽量缩减这些重复工作的。

先举个例子
若S = “aaaaaaaaaaab”, T = “aaaaab” 现在逐位进行比较，到第五位时就会失配。

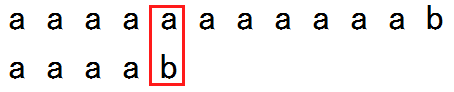
将T后移，若直接逐位比较，那么又要比较五次才会发现仍会在第五位失配

那么容易发现前四位的比较并不是必要的，为什么呢？我们会发现因为T[1…3] = T[2…4]，即S[1…3] = S[2…4],又已验证S[1…3] = T[1…3],所以S[2…4] = T[1…3]，再进行比较只会浪费时间。

再来一个更普遍的例子：
S = “abaaaababb”, T = “abaab”

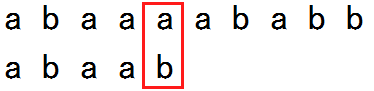
逐位比较，在第五位发现失配，下面可直接作出如下操作：

使之后直接进行“有用”的第二位操作。

可能有人会产生疑问，为什么T串要移动到这个位置？我们观察T串会发现，在已进行匹配的五位中，T[1…2] = T[4…5]，我们已发现S[4]与T[4]匹配，而T[1] = T[4]，故可将T[1]移到S[4]直接进行下一步比较。

下面介绍如何算出后移位数。

NEXT数组的计算

我们会发现，要后移的位数只与T串有关，找出T串相同的前缀和后缀长度（且不能为自己，想一想，为什么），即可以算出最佳的后移位数。
我们用next[x]表示当T的前x位最长相同前缀和后缀的长度，即当T第x位失配时应该后移x - next[x]位。
能不能直接求呢？当然可以，但这样同样太慢了，会使得KMP算法的优越性不复存在。
那么如何效率算出f数组呢？
我们假设已经计算好前7位，且next[7] = 3，现在计算第8位，如图所示

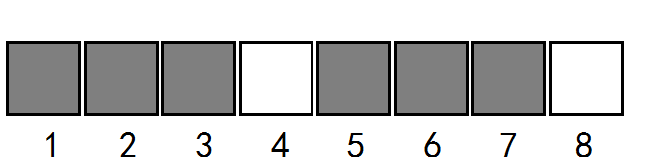
若此时T[4] = T[8]，可直接求出next[8] = next[7] + 1 = 4
然而有时情况并非这样，若T[4] != T[8]
那么我们查看next[next[7]]，即next[3]，我们假设next[3] = 2，即T[1…2] = T[2…3]，相应的，我们有T[5…6] = T[6…7]，他们与T[1…2]也相等。

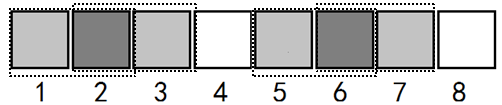
若此时T[3] = T[8]，即T[1…3] = T[6…8]，可直接求出next[8] = next[3]+1 = 3
但若T[3]！ = T[8]，我们继续查看next[next[3]],即next[2]

…（以此类推，进行“前缀的配置”直至配置成功，边界为next[0] = 0）

至此，你有没有懂next数组的计算原理了呢？多模拟上述过程，加强自己的理解。（*形成自己的理解很重要）
下面给出代码：

1
2
3
4
5
6
7
8
9
void Make_Next(char T[], int next[]) {
    int len = strlen(T);
    next[0] = 0;                                   //边界
    for (int i = 0, k = 0; i < len; i++) {
        while (k && T[i] != T[k]) k = next[k-1];   //上面图示过程，注意k为非负数
        if (T[i] == T[k]) k++;                     //进行匹配
        next[i] = k;                               //保存
    }
}

根据以上思路，我们自然而然的就可以写出整个程序了，在操作中，我们将“串的移动”操作为k指针的移动。下面给出代码参考。然而在继续阅读前，建议读者仿照上述思路先自己手写一遍代码。

[Code]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstring>
#include <iostream>
using namespace std;

const int maxn = 100;
int next[maxn];
char S[maxn], T[maxn];

void Make_Next() {
    int len = strlen(T);
    for (int i = 1, k = 0; i < len; i++) {
    while (k && T[i] != T[k]) k = next[k-1];
        if (T[i] == T[k]) k++;
        next[i] = k;
    }
}
bool Find() {
    int len1 = strlen(S), len2 = strlen(T);
    for (int i = 0, k = 0; i < len1; i++) {
    while (k && S[i] != T[k]) k = next[k];    //若失配，进行“前缀的配置”
        if (S[i] == T[k]) k++;
        if (k == len2) return true;           //找到子串，返回真
    }
    return false;
}
int main() {
    cin >> S >> T;
    Make_Next();
    if (Find()) cout << "Yes";
    else cout << "No";
    return 0;
}

完成后，相信你已发现制作next数组和查找子串的代码非常相似（这也是KMP算法的神奇之处之一）。你也可以稍微改动一下程序，使得程序输出T在S串中第一次出现的位置或出现的次数（这并不困难）。
至此，我们可以分析一下KMP算法的复杂度。我们可以这样看，应变量i和k在运算中不断增加直至达到字符串长度，所以KMP算法的复杂度线性的，已经达到很优。
KMP算法的优点在于代码短且复杂度低，而缺点有难于理解和代码容易打错，希望鄙人此文能有助于大家对于这一算法的理解。