Description
有n个询问(n≤50000),每个询问有五个整数a,b,c,d,k,求有多少个数对(x,y)满足a≤x≤b,c≤y≤d,且gcd(x,y)=k.(a≤b≤50000,c≤d≤50000,k≤50000)
Solution
我们发现,计算一个数x在某个闭区间[a,b]内的因数数量并不是很方便,可以转化为x在区间[1,b]的因数的数量-x在区间[1,a-1]的因数的数量(因为求[1,Z]比较好求)。
原问题是,对于所有x∈[a,b],y∈[c,d],求所有gcd(x,y)=k的点对的数量。
根据容斥原理,问题转化为,计算:
所有x∈[1,b],y∈[1,d],所有gcd(x,y)=k的点对的数量
-所有x∈[1,a-1],y∈[1,d],所有gcd(x,y)=k的点对的数量
-所有x∈[1,b],y∈[1,c-1],所有gcd(x,y)=k的点对的数量
+所有x∈[1,a-1],y∈[1,c-1],所有gcd(x,y)=k的点对的数量
所以怎么求解任意x∈[1,n],y∈[1,m],所有gcd(x,y)=k的点对的数量呢?
设f(k)=任意x∈[1,n],y∈[1,m],所有gcd(x,y)=k的点对的数量,我们发现并不好求,于是再设F(k)=任意x∈[1,n],y∈[1,m],所有满足k整除gcd(x,y)的点对的数量
因为F值比f值容易求,所以我们这时可以运用莫比乌斯反演了。
容易发现,只要是k的倍数的f值都对F(k)有贡献,即F(k)=∑k∣df(d)
我们可以知道F(k)=⌊kn⌋⌊km⌋,即n内有n/k个数是k的倍数,m内有n/k个数是k的倍数,他们两两之间的最小公因数一定包含k。
于是$$f(k)=\sum_{k|d}\mu(\frac{d}{k})\lfloor \frac{n}{d} \rfloor\lfloor \frac{m}{d} \rfloor$$
这样我们就可以在线性时间求出f的值了。
然而我们发现,每个询问的需要计算四个f,复杂度依然达到平方级,仍需优化。
还有哪里可以优化呢?
我们发现,其实有一些k,他们的⌊kn⌋⌊km⌋是一样的,我们还要对他们分别求和,拉慢了运行速度。
因为不同⌊kn⌋⌊km⌋值最多2∗(n+m)个(证明如下)
可以发现,⌊kn⌋的值最多2n个(小于n的因数x对应一个大于n的因数n/x),我们将⌊kn⌋值相等的k在数轴上分到一个区间,(如下图),则最多2n个区间,相同的,⌊km⌋的值最多2n值相等的k最多2m个区间。以n=6,m=8为例。
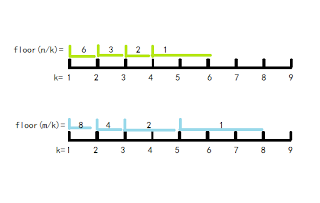
就是说,⌊kn⌋有2n取值,⌊kn⌋有3n取值,它们对应起来的取值,就是划分的2(kn+km)区间的区间。
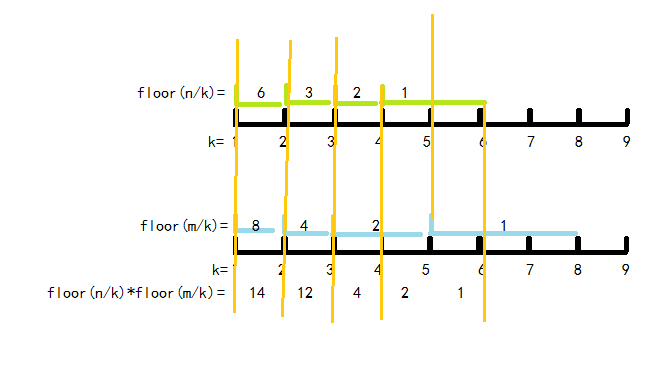
且⌊kn⌋⌊km⌋值相同的k显然是连续的,我们可以对μ求一下前缀和,对于值相同的k直接乘上他们的μ值和即可,这样就可以将复杂度优化到Θ(n∗max(b,d))了。
然而我们怎么找到每个区间的起点和终点呢?我们发现,m/k可以找到floor值为k的区间的末尾值,例如第一个数轴中6/floor(6/5)可以找到5所在区间的末尾6,第二个数轴中8/floor(8/5)可以找到5所在区间的末尾8,这样,区间起点为i,这个区间末尾就是min(floor(n/(n/i)),floor(m/(m/i))).
其实还可以更优化,求所有x∈[a,b],y∈[c,d],求所有gcd(x,y)=k的点对的数量可转化为x∈[a/k,b/k],y∈[c/k,d/k],求所有gcd(x,y)=1的点对的数量,只要在程序里加一句话就可以提速50%了,留给读者自己思考。
之后的事就非常愉快辣!
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=50000+10;
bool form[maxn];
int prime[maxn],mu[maxn]={0,1},sum[maxn],cnt;
void MakeMuList(){
for(int i=2;i<maxn;i++){
if(!form[i]) prime[cnt++]=i,mu[i]=-1;
for(int j=0;prime[j]*i<maxn;j++){
form[prime[j]*i]=true;
if(!(i%prime[j])){
mu[prime[j]*i]=0;
break;
}
mu[prime[j]*i]=-mu[i];
}
}
for(int i=1;i<maxn;i++) sum[i]=sum[i-1]+mu[i];
}
int f(int n,int m,int k){
int ans=0;
if(n>m) swap(n,m);
for(int i=1,last;i<=n;i=last+1){
last=min(n/(n/i),m/(m/i));
ans+=(sum[last]-sum[i-1])*(m/(i*k))*(n/(i*k));
}
return ans;
}
int main(){
MakeMuList();
int kase; scanf("%d",&kase);
while(kase--){
int a,b,c,d,k; scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
printf("%d\n",f(b,d,k)-f(a-1,d,k)-f(b,c-1,k)+f(a-1,c-1,k));
}
return 0;
}
|

