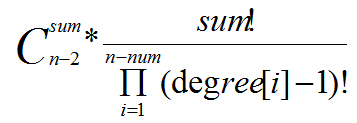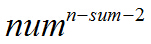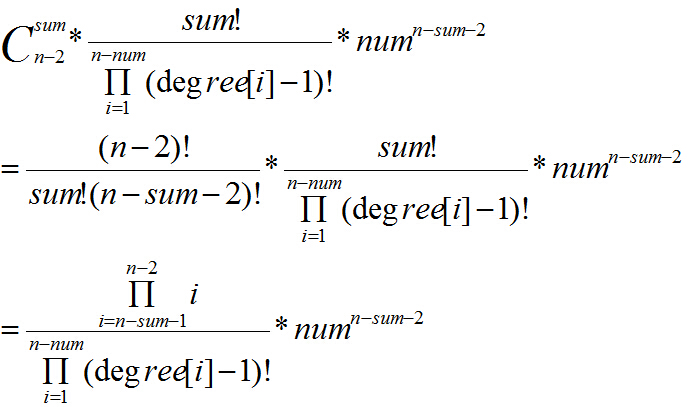Description
自从明明学了树的结构,就对奇怪的树产生了兴趣… 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N <= 1000),接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1.
Output
一个整数,表示不同的满足要求的树的个数,无解输出0.
Sample Input
Sample Output
HINT
两棵树分别为1 - 2 - 3; 1 - 3 - 2
Solutions
一道比较简单的组合数学题。
首先我们要了解一下Prufer Sequence(普吕弗序列)(内容摘自zyj PPT).
Prufer Sequence是一个和某棵结点数为n的树唯一对应的一个长度为n-2的整数序列。定义如下:
假定已知的n个顶点标志为1,2,…,n,假定T是其中的一棵树。设a1为叶节点中有标号最小者,与a1连接的点为b1,从T中消去点a1和边(a1,b1),再从余下的数T1中寻找标号最小的叶节点,设为a2,a2的邻接点为b2,从从T1中消去点a2和边(a2,b2)。如此步骤n-2次,直到最后剩下一条边为止。于是一棵树T对应一序列:b1,b2,…,bn-2
这些数是1~n中的数,并且允许重复。
相反地,用b1,b2…bn-2可以恢复树T本身,因为消去的是树叶中标号最小的,而且它和b1是邻接的。
即给出一序列b1,b2,…,bn-2,其中1<=bi<=n,i=1,2,…,n-2.可恢复与之对应的树,方法如下:
有两个序列,一个是(1)1,2,…,n,另一个是(2)b1,b2,…,bn-2
在序列(1)中找出第一个不出现在序列(2)b1,b2,…,bn-2中的数,这个数显然便是a1,同时形成边(a1,b1),并从(1)中消去a1,从(2)中消去b1。在余下的(1)和(2)中继续以上的步骤n-2次,直到序列(2)为空集为止。这时序列(1)中剩下的两个数x,y,边(x,y)就是树T的最后一条边。
看不懂? 来看个栗子
树T
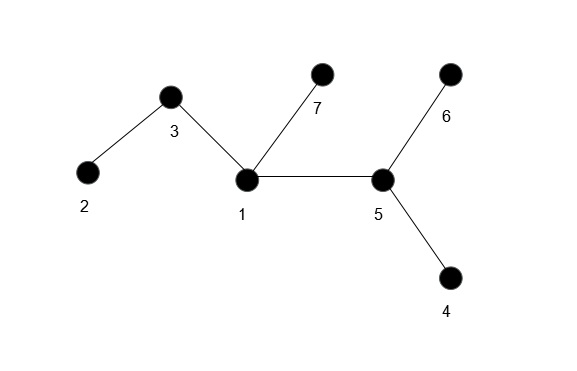
找编号最小的节点,为2,与他相连的为3,将3加入序列

消掉点2和边(2,3),找到当前编号最小的节点,为3,与他相连的为1,将1加入序列
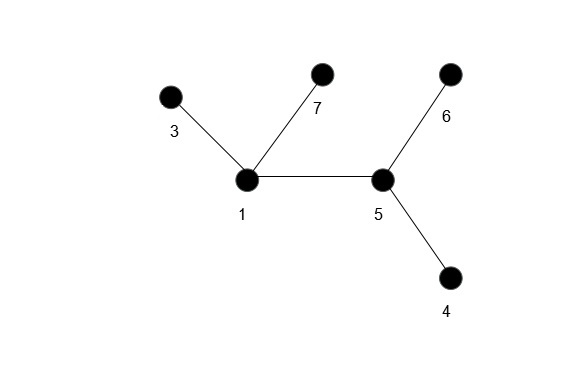

重复这个操作
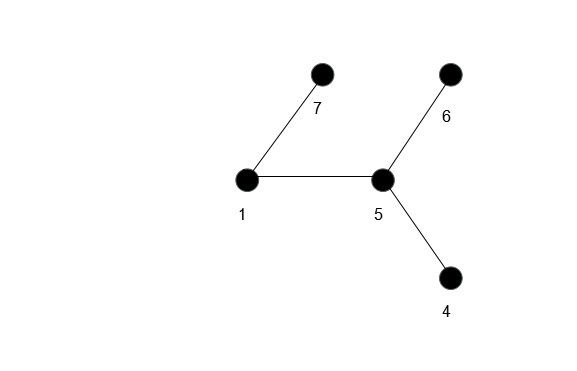

… 直到最后得到这个序列

同样,我们用这个序列恢复这棵树
现有(1,7)之前并未消去
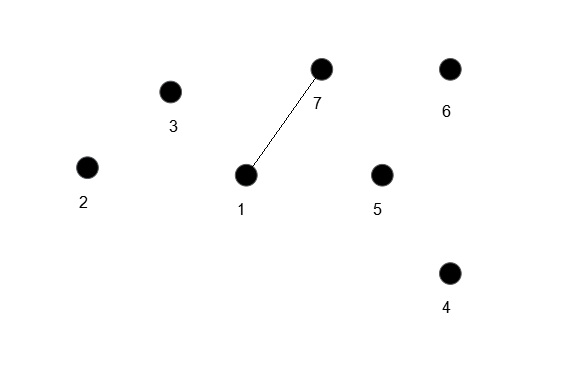
开始操作

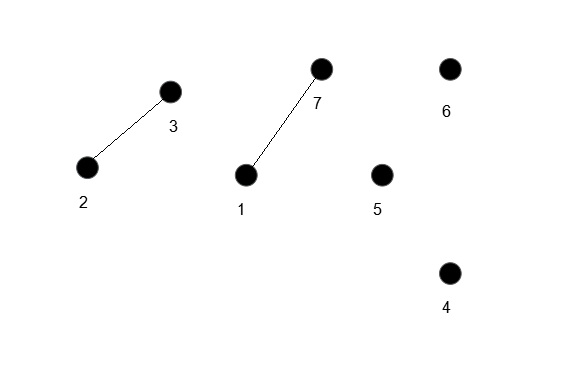

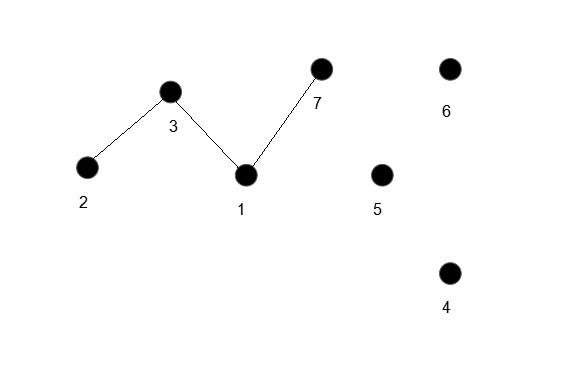

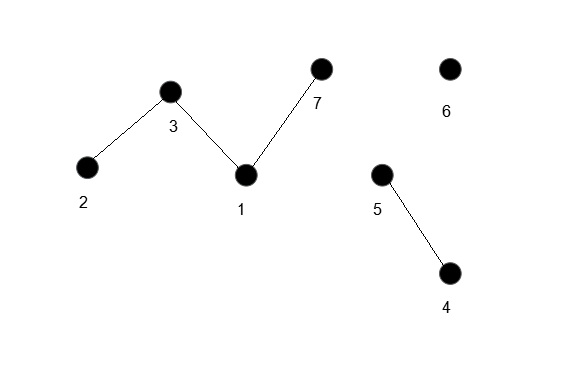

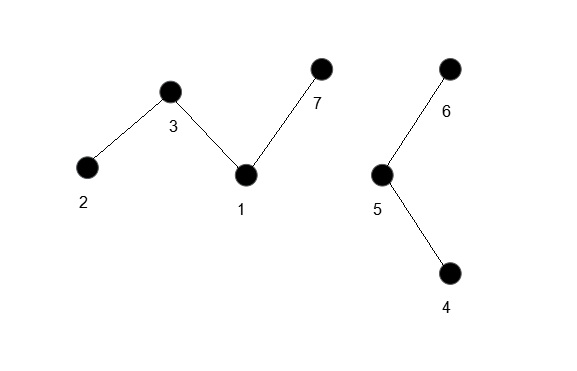

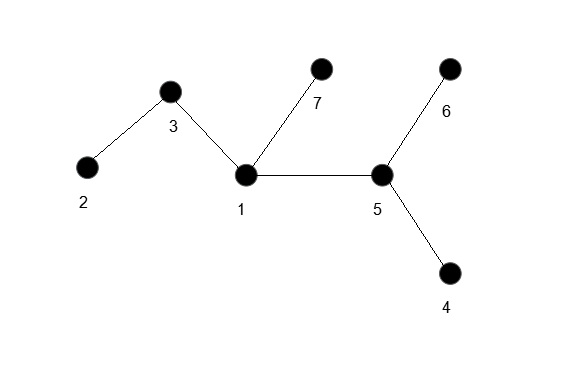
这样很容易看出,每一个Prufer Sequence对应一颗唯一的树(一一对应)。
回到题目中来。
我们发现,树中结点的度和结点号在此序列中出现的次数有关(结点i在序列中出现的次数=degree[i]-1).
由题意,有题目给出度数的限制,同时也就限制了序列的一些条件。树的所有可能情况也就是序列可能的情况。
设度数没有限制的点的数量为num,有限制的点在序列中出现的总次数为sum
可知,n-num个没有限制的点在序列中的排列总情况为
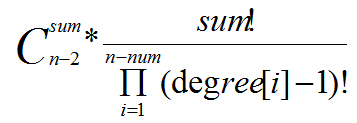
(从n-2个位置选sum个位置填充这些数*排列方式为多重集的全排列方案数)
剩下n-sum-2 个位置可由num个数填充,方案数为
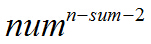
所以答案为
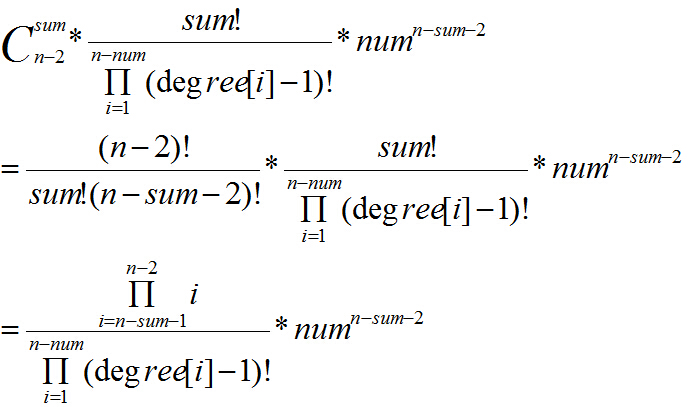
因为可能爆long long,用分解质因数求以下就可以了。
然后答案也比较畸形,要用高精度,好像要开3000位,不然就神作了。
注意当任意degree=0时是无解的。
另外,当sum>n-2同样也是无解的。
注意特判n=1的情况,if(degree[1]=0) ans=1, else ans=0;
然后就可以愉快的AC辣–
附一段代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include<cstdio>
#include<cctype>
inline int readint(){
int x=0; char c=getchar(); bool minu=false;
while(!isdigit(c) && c!= '-') c=getchar();
if(c=='-') minu=true; else x=c-'0';
while(isdigit(c=getchar())) x=(x*10)+c-'0';
return minu?-x:x;
}
const int maxn=1000+10;
int degree[maxn];
int form[maxn],prime[maxn],facnum[maxn],cnt;
void MakePrimeList(int n){
for(int i=2;i<=n;i++) if(!form[i]){
prime[cnt++]=i;
for(int j=i*i;j<=n;j+=i) form[j]=true;
}
}
long long pow(long long a,int n){
long long ans=1;
while(n){
if(n&1) ans*=a;
a*=a; n>>=1;
}
return ans;
}
void fac(int x,int t){
if(!x || !t) return;
for(int i=0;i<cnt;i++)
while(!(x%prime[i])) facnum[i]+=t,x/=prime[i];
}
long long ans[3000]={1},digit=1;
void count(){
for(int i=0;i<cnt;i++) if(facnum[i]){
int x=0;
for(int k=0;k<facnum[i];k++){
for(int j=0;j<digit;j++) ans[j]*=prime[i];
for(int j=0;j<digit;j++){
ans[j]+=x;
x=ans[j]/10;
ans[j]%=10;
}
while(x) ans[digit++]=x%10,x/=10;
}
}
}
int main(){
int n=readint(),sum=0,num=0;
MakePrimeList(maxn);
if(n==1){
if(readint()) putchar('0'); else putchar('1');
return 0;
}
for(int i=0;i<n;i++){
degree[i]=readint();
if(!degree[i]) { printf("0"); return 0; }
else if(degree[i]==-1) num++;
else sum+=degree[i]-1;
}
if(sum>n-2) { printf("0"); return 0; }
fac(num,n-sum-2);
for(int i=n-sum-1;i<=n-2;i++) fac(i,1);
for(int i=0;i<n;i++) if(degree[i]!=1)
for(int j=2;j<degree[i];j++) fac(j,-1);
count();
for(int i=digit-1;i>=0;i--) putchar(ans[i]+'0');
return 0;
}
|
然后 BZOJ11211 就是简化了的题目了(建议先完成)